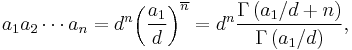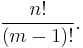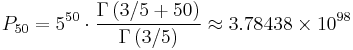Arithmetic progression
In mathematics, an arithmetic progression (AP) or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant. For instance, the sequence 3, 5, 7, 9, 11, 13, … is an arithmetic progression with common difference 2.
If the initial term of an arithmetic progression is 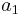 and the common difference of successive members is d, then the nth term of the sequence is given by:
and the common difference of successive members is d, then the nth term of the sequence is given by:
and in general
A finite portion of an arithmetic progression is called a finite arithmetic progression and sometimes just called an arithmetic progression.
The behavior of the arithmetic progression depends on the common difference d. If the common difference is:
- Positive, the members (terms) will grow towards positive infinity.
- Negative, the members (terms) will grow towards negative infinity.
Contents |
Sum
The sum of the members of a finite arithmetic progression is called an arithmetic series.
Expressing the arithmetic series in two different ways:
Adding both sides of the two equations, all terms involving d cancel:
Dividing both sides by 2 produces a common form of the equation:
An alternate form results from re-inserting the substitution: 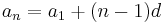 :
:
In 499 CE Aryabhata, a prominent mathematician-astronomer from the classical age of Indian mathematics and Indian astronomy, gave this method in the Aryabhatiya (section 2.18) .[1]
So, for example, the sum of the terms of the arithmetic progression given by an = 3 + (n-1)(5) up to the 50th term is
Product
The product of the members of a finite arithmetic progression with an initial element a1, common differences d, and n elements in total is determined in a closed expression
where 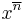 denotes the rising factorial and
denotes the rising factorial and 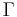 denotes the Gamma function. (Note however that the formula is not valid when
denotes the Gamma function. (Note however that the formula is not valid when 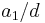 is a negative integer or zero.)
is a negative integer or zero.)
This is a generalization from the fact that the product of the progression 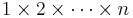 is given by the factorial
is given by the factorial 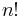 and that the product
and that the product
for positive integers  and
and  is given by
is given by
Taking the example from above, the product of the terms of the arithmetic progression given by an = 3 + (n-1)(5) up to the 50th term is
References
- ^ Aryabhatiya Marathi: आर्यभटीय, Mohan Apte, Pune, India, Rajhans Publications, 2009, p.95, ISBN 978-81-7434-480-9
- Sigler, Laurence E. (trans.) (2002). Fibonacci's Liber Abaci. Springer-Verlag. pp. 259–260. ISBN 0-387-95419-8.
See Also
- Geometric progression
- Generalized arithmetic progression - is a set of integers constructed as an arithmetic progression is, but allowing several possible differences.
- Harmonic progression
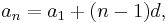
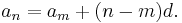
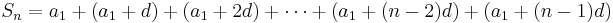
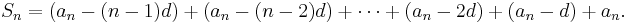
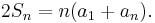
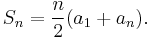
![S_n=\frac{n}{2}[ 2a_1 %2B (n-1)d].](/2012-wikipedia_en_all_nopic_01_2012/I/7456a8d727899b701af9e209bed95cdc.png)
![S_{50} = \frac{50}{2}[2(3) %2B (49)(5)] = 6,275.](/2012-wikipedia_en_all_nopic_01_2012/I/7e0db06c81a39073a72702fbe14eb3a5.png)